An Introduction to Numba for Bioinformatics
Test Installation
import sys
sys.version
'3.6.3 | packaged by conda-forge | (default, Nov 4 2017, 10:13:32) \n[GCC 4.2.1 Compatible Apple LLVM 6.1.0 (clang-602.0.53)]'
import numpy as np
np.version.version
'1.14.2'
import numba
numba.__version__
'0.36.2'
import math
import matplotlib.pyplot as plt
from collections import Counter
%matplotlib inline
What is Numba
Numba gives you the power to speed up your applications with high performance functions written directly in Python. With a few annotations, array-oriented and math-heavy Python code can be just-in-time compiled to native machine instructions, similar in performance to C, C++ and Fortran, without having to switch languages or Python interpreters.
Numeric Data
Pure Python
list_of_lists = [list(np.random.rand(2500)) for i in range(2500)]
print(len(list_of_lists), len(list_of_lists[0]))
2500 2500
def python_sum_of_squares_list(input_arr):
result = 0
num_rows, num_cols = len(input_arr), len(input_arr[0])
for i in range(num_rows):
for j in range(num_cols):
result += input_arr[i][j]**2
return result
python_sum_of_squares_list(list_of_lists)
2082606.0782765413
%timeit -n 2 -r 2 python_sum_of_squares_list(list_of_lists)
2.64 s ± 24.4 ms per loop (mean ± std. dev. of 2 runs, 2 loops each)
Using numpy arrays
numpy_array = np.array(list_of_lists)
print(numpy_array.shape)
(2500, 2500)
def numpy_loop_sum_of_squares_array(input_arr):
result = 0
num_rows, num_cols = input_arr.shape
for i in range(num_rows):
for j in range(num_cols):
result += input_arr[i, j]**2
return result
numpy_loop_sum_of_squares_array(numpy_array)
2082606.0782765413
%timeit -n 2 -r 2 numpy_loop_sum_of_squares_array(numpy_array)
3.45 s ± 65.3 ms per loop (mean ± std. dev. of 2 runs, 2 loops each)
Numpy vectorization
def numpy_vectorized_sum_of_squares_array(input_arr):
return np.sum(input_arr**2)
numpy_vectorized_sum_of_squares_array(numpy_array)
2082606.0782765397
%timeit numpy_vectorized_sum_of_squares_array(numpy_array)
24 ms ± 654 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
numba.jit
@numba.jit
def numba_sum_of_squares_array(input_arr):
result = 0
num_rows, num_cols = input_arr.shape
for i in range(num_rows):
for j in range(num_cols):
result += input_arr[i,j]**2
return result
numba_sum_of_squares_array(numpy_array)
2082606.0782765413
%timeit numba_sum_of_squares_array(numpy_array)
7.66 ms ± 341 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
Contrived example:
2 matrices, if 1st > 2nd, 1st^2 - sqrt(2nd), otherwise 2nd^2 - sqrt(1st)
def square_or_sqrt(in1, in2):
num_rows, num_cols = in1.shape
output_arr = np.zeros((num_rows, num_cols))
for i in range(num_rows):
for j in range(num_cols):
if in1[i, j] > in2[i, j]:
output_arr[i, j] = (in1[i,j] ** 2) - math.sqrt(in2[i,j])
else:
output_arr[i, j] = (in2[i,j] ** 2) - math.sqrt(in1[i,j])
return output_arr
numpy_array_2 = np.random.rand(2500, 2500)
%timeit -n 1 -r 1 square_or_sqrt(numpy_array, numpy_array_2)
8.82 s ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
numba.vectorize
@numba.vectorize([numba.float64(numba.int64, numba.int64), numba.float64(numba.float64, numba.float64)])
def numba_square_or_sqrt(in1, in2):
if in1 > in2:
return (in1 ** 2) - math.sqrt(in2)
else:
return (in2 ** 2) - math.sqrt(in1)
%timeit numba_square_or_sqrt(numpy_array, numpy_array_2)
34.9 ms ± 4.5 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
p = square_or_sqrt(numpy_array, numpy_array_2)
n = numba_square_or_sqrt(numpy_array, numpy_array_2)
np.sum(p), np.sum(n)
(-207598.87433288957, -207598.87433288957)
Sequence Data
sequence = np.random.choice(np.array(tuple("ACGT"), dtype="S1"), 50000000)
print(sequence[:21].view("S3"))
[b'GGT' b'GCC' b'GCC' b'AGC' b'AAC' b'TAG' b'AGG']
string_sequence = sequence.tostring().decode()
string_sequence[:20]
'GGTGCCGCCAGCAACTAGAG'
Replace T with U
%timeit string_sequence.replace("T", "U")
184 ms ± 4.51 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
t = ord("T")
u = ord("U")
t, u
(84, 85)
@numba.vectorize([numba.int8(numba.int8)])
def replaceTU(x):
if x == t:
return u
else:
return x
%timeit replaceTU(sequence.view("int8"))
19.8 ms ± 474 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
Kmerization
def python_kmerize(sequence, k):
length_sequence = len(sequence)
kmers = [sequence[i:i+k] for i in range(length_sequence-k+1)]
return kmers
%timeit python_kmerize(string_sequence, k=20)
20.9 s ± 1.04 s per loop (mean ± std. dev. of 7 runs, 1 loop each)
@numba.jit
def numba_kmerize(sequence, k):
kmers = np.zeros((sequence.shape[0]-k+1, k), dtype="int8")
length_sequence = sequence.shape[0]
for i in range(length_sequence-k+1):
kmers[i] = sequence[i: i+k]
return kmers
%timeit numba_kmerize(sequence.view("int8"), k=20)
2.45 s ± 60.9 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
Parallel
parallel=True
numba.prange instead of range
numba.config.NUMBA_NUM_THREADS
4
@numba.jit(parallel=True)
def p_numba_kmerize(sequence, k):
kmers = np.zeros((sequence.shape[0]-k+1, k), dtype="int8")
for i in numba.prange(sequence.shape[0]-k+1):
kmers[i] = sequence[i: i+k]
return kmers
%timeit p_numba_kmerize(sequence.view("int8"), k=20)
781 ms ± 41.5 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
Alignments
def get_sequences_from_fasta(fasta_file: str) -> dict:
sequences = {}
with open(fasta_file) as f:
current_sequence = ""
current_key = None
for line in f:
if line.startswith(">"):
if current_key is None:
current_key = line.split(">")[1].strip()
else:
sequences[current_key] = current_sequence
current_sequence = ""
current_key = line.split(">")[1].strip()
else:
current_sequence += line.strip()
sequences[current_key] = current_sequence
return sequences
sequences_fasta = get_sequences_from_fasta("PF02238_full.fasta")
keys = list(sequences_fasta.keys())
sequences = list(sequences_fasta.values())
n_sequences = np.array([[ord(x) for x in seq] for seq in sequences], dtype="int8")
n_sequences.shape
(711, 102)
Find pairwise distance matrix
def python_pairwise_distance(sequence_1, sequence_2):
num_mismatches = 0
length_sequence = len(sequence_1)
for i in range(length_sequence):
if sequence_1[i] != sequence_2[i]:
num_mismatches += 1
return num_mismatches/length_sequence
def python_distance_matrix(sequences):
num_sequences = len(sequences)
matrix = np.zeros((num_sequences, num_sequences))
for i in range(num_sequences):
for j in range(num_sequences):
matrix[i, j] = python_pairwise_distance(sequences[i], sequences[j])
return matrix
p = %timeit -o -n 2 -r 2 python_distance_matrix(sequences)
5.84 s ± 58.9 ms per loop (mean ± std. dev. of 2 runs, 2 loops each)
@numba.jit
def numba_pairwise_distance(sequence_1, sequence_2):
num_mismatches = 0
length_sequence = sequence_1.shape[0]
for i in range(length_sequence):
if sequence_1[i] != sequence_2[i]:
num_mismatches += 1
return num_mismatches/length_sequence
@numba.jit(parallel=True)
def numba_distance_matrix(sequences):
num_sequences = sequences.shape[0]
matrix = np.zeros((num_sequences, num_sequences))
for i in numba.prange(num_sequences):
for j in numba.prange(num_sequences):
matrix[i, j] = numba_pairwise_distance(sequences[i], sequences[j])
return matrix
n = %timeit -o numba_distance_matrix(n_sequences)
9.48 ms ± 212 µs per loop (mean ± std. dev. of 7 runs, 1 loop each)
p.best/n.best
626.3191265320067
n_distmat = numba_distance_matrix(n_sequences)
distmat = python_distance_matrix(sequences)
plt.imshow(n_distmat, cmap="hot")
<matplotlib.image.AxesImage at 0x109c55c18>
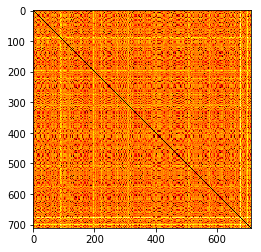
plt.imshow(distmat, cmap="hot")
<matplotlib.image.AxesImage at 0x132d34828>
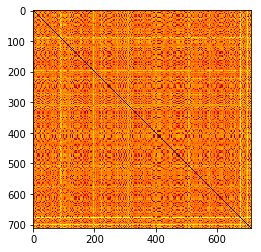
Find consensus sequence and consensus amino acid frequencies
def python_consensus(sequences):
len_alignment = len(sequences[0])
num_sequences = len(sequences)
counter_per_position = []
for i in range(len_alignment):
counts = []
for j in range(num_sequences):
counts.append(sequences[j][i])
counter = Counter(counts)
for c in counter:
counter[c] /= len(counts)
counter_per_position.append(counter.most_common()[0])
consensus_sequence = "".join(c[0] for c in counter_per_position)
consensus_frequencies = [c[1] for c in counter_per_position]
return consensus_sequence, consensus_frequencies
%timeit python_consensus(sequences)
17.6 ms ± 399 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
py_seq, py_freqs = python_consensus(sequences)
@numba.jit(parallel=True)
def numba_consensus(sequences):
sequences_t = sequences.T
consensus = np.zeros((sequences_t.shape[0], 256), dtype="i8")
for i in numba.prange(sequences_t.shape[0]):
for letter in sequences_t[i]:
consensus[i,letter] += 1
return np.argmax(consensus, axis=1).astype("int8").view("S1"), np.max(consensus, axis=1)/sequences_t.shape[1]
%timeit numba_consensus(n_sequences)
241 µs ± 37.9 µs per loop (mean ± std. dev. of 7 runs, 1 loop each)
n_seq, n_freqs = numba_consensus(n_sequences)
n_seq = n_seq.tostring().decode()
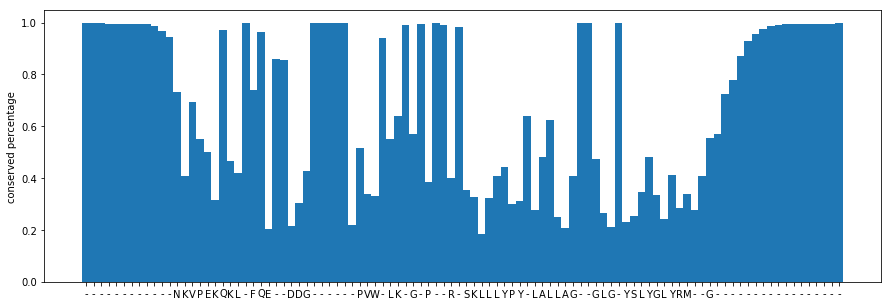
def plot_consensus(consensus_sequence, consensus_frequencies):
plt.bar(range(len(consensus_sequence)), consensus_frequencies, width=1)
plt.xticks(range(len(consensus_sequence)), list(consensus_sequence))
plt.ylabel("conserved percentage")
plt.figure(figsize=(15,5))
plot_consensus(n_seq[:100], n_freqs[:100])
Advanced
Using more than one element
@numba.guvectorize and @numba.stencil
Use neighboring elements, kernels, by row, by column etc.
Classes
Let’s you use python class syntax (methods, properties/attributes)
C functions
- C-functions with pure Python syntax
- Cleaner syntax than Cython
- Can go low-level
Ahead-of-time compilation
Compiled extension module that can be run on computers without Numba installed.
Numba for CUDA GPUs (in python syntax)
Limitations
- Error messages without traceback (start in pure Python, then jit)
- No dictionary or set support (fast in Python anyway). Supported Python features
- Limited class support (call jit-functions from classes)
- Parallelization can break sometimes (with reason)